|
|
|
| Vita |
| Pubblicazioni |
| Prossimi eventi |
|
|
| Filosofia antica | |
| Mistica | |
| Sufismo | |
| Taoismo | |
| Vedanta | |
| Buddhismo | |
| Zen | |
| Filosofia Comparata | |
| Musica / Mistica | |
| Filosofia Critica | |
| Meditazione | |
| Alchimia | |
| Psiché | |
| Tantrismo | |
| Varia | |
|
| Mircea Eliade |
| Raimon Panikkar |
| S.Weil e C.Campo |
| René Guénon, ecc. |
| Elémire Zolla |
| G.I.Gurdjieff |
| Jiddu Krishnamurti |
| Rudolf Steiner |
| P. C. Bori |
| Silvano Agosti |
| Alcuni maestri |
Ex nihilo omnia (Piergiorgio Odifreddi)
Non vogliamo certo parlare di nulla: o meglio, certo vorremmo parlare di nulla, ma ce lo impedisce formalmente la sintassi italiana. Passare alla semantica non risolve però il problema, e lo rende anzi ancora più problematico: a meno che non ci si limiti a profondità abissali quali il fatto che il nulla non è per nulla essere, o che l'essere sta dove non sta il nulla, e via di seguito.
Se sintassi e semantica sembrano inadeguate al trattamento di un concetto quale il nulla, imbrigliandolo in maglie troppo strette, le metafore rischiano di allargarne a dismisura la concezione: la quiete, l'interruzione, la rinuncia, la paralisi, l'assenza, la partenza, la fuga, la scomparsa, la morte, la dissoluzione, la decomposizione, l'annichilazione, l'esplosione, la distruzione, la fine, ... sono tutte immagini di un'avvicinamento al nulla, così come il principio, la creazione, la nascita, l'arrivo, il ritorno, l'apparizione, la presenza, la conservazione, la preservazione, la continuazione, il movimento, l'azione, l'impegno, ... sono invece immagini di un allontanamento da esso.
Per evitare i pericoli contrapposti del vuoto discorso e della metafora illimitata, ci concentreremo quindi sulle metamorfosi del concetto di nulla nei campi in cui esse sono state più feconde e profonde, e cioè nell'arte, in filosofia, nella fisica e nella matematica.
1 Il silenzio dell'arte
L'arte è un mezzo per esprimere ciò che si sente: poichè in condizioni dapprima eccezionali, e poi sempre più comuni, il sentire di alcune `civiltà' è l'alienazione, il nulla ha acquistato un ruolo consistente nelle loro rappresentazioni artistiche.
Parole
La prima apparizione letteraria del nulla è forse nel libro ix dell'Odissea : dopo essere rimasto intrappolato nella grotta di Polifemo con i suoi compagni, Ulisse (Odisseus: OdnsseuV) dice astutamente al ciclope di chiamarsi Nessuno (Oudeis: OudeiV),1 e lo acceca; quando gli altri ciclopi accorrono alle urla di Polifemo e gli domandano se abbia bisogno di aiuto, egli risponde che Nessuno gli sta facendo del male; l'equivoco impedisce loro di aiutarlo, e permette invece ad Ulisse di attendere l'occasione propizia per fuggire.
In seguito il nulla divenne una costante di riferimento della letteratura tragica: dai classici greci che lo subirono nell'amaro destino, ai romantici ottocenteschi che lo corteggiarono con nostalgica malinconia. In casa nostra un campione di questo atteggiamento fu Giacomo Leopardi, nel cui canto Ad Angelo Mai il nulla affiora come immagine universale: della condizione umana (``a noi presso la culla, immoto siede, e su la tomba, il nulla'', 74-75), della conoscenza (``discoprendo, solo il nulla s'accresce'', 99-100), e della realtà stessa (``ombra reale e salda ti parve il nulla'', 130-132). E sul tema egli ritornò frequentemente, da La ginestra (``questo globo ove l'uomo è nulla'', 172-173) allo Zibaldone (``il principio delle cose, e di Dio stesso, è il nulla''; ``tutto è nulla al mondo, anche la mia disperazione''; ``è un nulla anche questo mio dolore'').
Nella direzione opposta alla tragicità, i nonsense di Lewis Carroll mostrano invece come il nulla possa avere effetti comici devastanti. In Alice nel paese delle meraviglie ad Alice viene offerto del vino inesistente; il gatto del Cheshire svanisce lentamente, fino a che non ne rimane nulla se non il ghigno; e la regina pretende che si decapiti la testa del gatto, benchè essa non abbia un corpo. In Attraverso lo specchio dapprima il Re Bianco si stupisce che Alice abbia la vista così buona da riuscire a vedere che nessuno è in arrivo; e quando il messaggero arriva senza aver superato nessuno, il re conferma che questi è stato visto anche da Alice, e deduce che nessuno cammina più lento del messaggero, altrimenti sarebbe arrivato prima di lui.
Passando dal nulla stesso alle sue metafore, la più nota è certo il nichilismo : un termine inizialmente introdotto nel 1862 da Turgenev in Padri e figli , per indicare il rifiuto radicale dei valori stabiliti che caratterizza il conflitto generazionale. Detto dai padri, biologici o spirituali, ``siete tutti nichilisti'' significa dunque: ``non rispettate nulla'' (beninteso, ``di ciò che noi rispettiamo''). Raccontato dai letterati, il nichilismo raggiunse il suo apice nell'ottocento nei romanzi di Dostoievski, in particolare negli atteggiamenti di personaggi quali Raskolnikov in Delitto e castigo , Stavrogin nei Demoni , e Ivan nei Fratelli Karamazov . Nel novecento il nichilismo letterario subì poi varie metamorfosi, dalla ``generazione perduta'' di Gertrude Stein alla ``gioventù bruciata'' di James Dean, per culminare infine nella letteratura esistenzialista francese dell'ultimo dopoguerra, da La nausea di Jean Paul Sartre a Lo straniero di Albert Camus.
Un altra metafora quasi scontata del nulla è il tema dell' assenza : e le opere che parlano di qualcuno che non c'è o non arriva abbondano, dai Sei personaggi in cerca di autore di Luigi Pirandello all'Aspettando Godot di Samuel Beckett.
Altrettanto immediata è la metafora dell'ombra : dalla Storia straordinaria di Peter Schlemihl di Adelbert von Chamisso, del 1812, a Peter Pan e Wendy di James Matthew Barrie, del 1911, sino al film Luna e l'altra di Maurizio Nichetti, del 1997, si narrano le avventure di ombre che si staccano dai rispettivi corpi e acquistano vita propria.
Una terza ovvia metafora del nulla è il buco . Nell'era elisabettiana con `nulla' si intendeva più precisamente quel buco primordiale e prototipale che è la vagina: il che permise allora a William Shakespeare di descrivere le tresche amorose come Tanto rumore per nulla , e permette a noi ora di annettere ai discorsi sul nulla buona parte della letteratura mondiale. Rimanendo però più sul letterale, come opere sui buchi si possono citare: Il tunnel di Dürrenmatt, del 1952; Yellow submarine di George Dunning, del 1968, che è il viaggio dei Beatles nel mare dei buchi; e Chi ha incastrato Roger Rabbit di Robert Zemeckis, del 1982 (in entrambi i film al momento opportuno dei buchi vengono estratti da una tasca provvidenziale, e applicati al muro per permettere la fuga in situazioni disperate).
Se però assenze, ombre e buchi sono metafore letterarie del nulla, solo il silenzio ne è la realizzazione letterale. Il silenzio della mente è stato elogiato da Socrate (``tutto ciò che so è che non si può sapere nulla'') e da Chuang Tzu (``il vero sapere è sapere che ci sono cose che non si possono sapere''). Al silenzio della bocca hanno invece incitato memorabilmente Lao Tze con il ``chi sa non parla, chi parla non sa'' (Tao Tze Ching , lxxxi), e Wittgenstein con il ``su ciò di cui non si può parlare, si deve tacere'' (Tractatus , 7). Quest'ultimo era però già stato anticipato e superato nel 1786 da Lorenzo da Ponte, librettista delle Nozze di Figaro : di fronte all'accusa di essersi ispirato ad un'opera di Beaumarchais bandita dalla corte, egli si era infatti giustificato sostenendo che ``su ciò di cui non si può parlare, si può cantare'', suggerendo che le limitazioni del linguaggio possono essere superate da una sua estensione quale il canto, che non è solo linguaggio (essendo anche musica).
Una realizzazione pratica del silenzio può essere l'opera letteraria non stampata, non terminata o addirittura non scritta, di cui esistono svariati esempi: i grandi profeti, da Socrate a Cristo, hanno solo parlato; il famoso secondo libro della Poetica di Aristotele forse non è mai stato scritto; libri certamente mai scritti sono stati recensiti da Jorge Luis Borges in Finzioni , e da Stanislav Lem in Vuoto perfetto ; Marcel Bénabou ha analizzato la sua inesistente produzione in Perchè non ho scritto nessuno dei miei libri , di cui viene detto e ripetuto che non è un libro; Suburbia , di Paul Fournel, è un'opera completa di prefazione, introduzione, note, postfazione, indice ed errata corrige, ma non di testo; gli ultimi due capitoli, il xviii e il xix, del Tristam Shandy di Laurence Sterne consistono di fogli bianchi, così come il Saggio sul silenzio di Elbert Hubbard, la monografia Serpenti delle Hawaii dello Zoo di Honolulu, e il The n \bigcircthing book che viene venduto negli Stati Uniti.
Suoni
Se nella musica, secondo Da Ponte, il canto può essere considerato una forma paradossale e metaforica di silenzio, la pausa ne è una versione letterale, e svolge nella notazione musicale un ruolo analogo a quello dello spazio fra parole nella scrittura moderna (nella scrittura antica, così come nel parlato, le parole non sono staccate fra loro), o dello zero nella notazione numerica. A differenza di questa, però, in cui le ripetizioni di 0 sono indicate per esteso, in musica ci sono otto tipi di pause (breve, semibreve, minima, semiminima, croma, semicroma, biscroma, semibiscroma), ciascuna di durata doppia della seguente: esse possono essere seguite da un punto (che ne moltiplica il valore per 1,5), o sovrastate da una corona (che ne prolunga il valore arbitrariamente), ma non collegate da una legatura.
La composizione musicale che ha più sfruttato il silenzio è 4'33'' di John Cage, che si articola in tre movimenti: 30'' , 2'23'' e 1'40'' . La durata totale è di 273'', che sono un esplicito richiamo ai -273° di quell'altra forma di nulla che è lo zero assoluto, a cui ritorneremo più oltre. La poetica di Cage era comunque non tanto quella di suonare il non suono, quanto di mostrare che il silenzio assoluto non esiste, o almeno non è purtroppo di questa terra (come il regno dei cieli): una qualunque esecuzione del silenzio si scontra infatti contro gli inevitabili rumori di fondo dell'ambiente e del pubblico, ed è dunque una pratica dimostrazione della propria teorica irrealizzabilità.
Il passo successivo al silenzio puro è la composizione con un solo suono: essa è stata realizzata nella Sinfonia monotona di Yves Klein, del 1947, che consiste di un lungo suono continuo seguito da un lungo silenzio. L'idea in questo caso è che un suono prolungato o ripetuto finisce per essere rimosso dall'apparato uditivo, e diventa dunque a tutti gli effetti un analogo del silenzio; viceversa, la mancanza di un suono o di un rumore a cui ci si è abituati viene invece percepita effettivamente, come se fosse un suono.
Anche il rumor bianco , che si ottiene per somma di tutti i possibili suoni, è una forma di silenzio. Matematicamente, la possibilità di ottenere il silenzio dalla composizione di suoni è una versione del fatto che la funzione costante di valore 0 si può scrivere in serie di Fourier, come somma di funzioni sinusoidali di varia ampiezza e periodo.
Immagini
Come il silenzio è l'assenza di suono, così il color nero è l'assenza di colore, e il buio è l'assenza di luce. All'estremo opposto, analoghi del rumor bianco che contiene tutti i suoni sono invece il color bianco e la luce , che contengono tutti i colori (come mostra l'esperimento del prisma che decompone la luce bianca nello spettro delle varie lunghezze d'onda corrispondenti ai vari colori).
Il ruolo della pausa nella musica è preso nella pittura da porzioni del colore di fondo del foglio o della tela su cui si disegna o si dipinge, e analoghi del silenzio sono i quadri non dipinti di Lucio Fontana, che alla mancanza di pittura uniscono anche buchi o tagli che rappresentano il vuoto. Alle composizioni ad un solo suono corrispondono invece le tele monocrome bianche, nere o blu di artisti quali Robert Rauschenberg, Ad Reinhardt e Yves Klein.
Naturalmente, qualunque raffigurazione pittorica (e, più in generale, iconica 2) è un simulacro del nulla: anche se le immagini sulla tela pretendono infatti di rappresentare qualcosa, non per questo esse cessano di essere segni, e dunque niente di ciò che è rappresentato. Il concetto è stato espresso in maniera memorabile da Magritte con Il tradimento delle immagini : un disegno di una pipa con la scritta Ceci n'est pas une pipe , ad indicare da un lato che la scritta non è la raffigurazione, e dall'altro che la raffigurazione non è l'oggetto raffigurato. E proprio sull'ambiguità tra i vari livelli si giocano i giochi delle rappresentazioni apertamente paradossali del surrealismo, così come delle rappresentazioni apparentemente consistenti dei paradossi percettivi alla Escher.
2 Il nulla della filosofia
In un senso ristretto, `nichilismo' significa rifiuto di concetti o valori accettati dal pensiero e dalla morale convenzionali: essendo i conservatori la maggioranza e al potere, eccetto che nei momenti di gloria delle ghigliottine, il termine fu dunque solitamente usato con una connotazione polemica e denigratoria (da Jacobi contro l'idealismo, da Jean Paul contro il romanticismo, da von Baader contro il protestantesimo, da Donoso Cortés contro il socialismo, ...). Nel senso generico di affermazione del nulla o di negazione dell'essere, che più ci interessa qui, il nichilismo ha invece permeato la storia della filosofia.
Assolutamente nulla
Il nulla si può anzitutto concepire in maniera relativa, come non essere qualcosa : in tale prosaica e (letteralmente) platonica concezione esso presuppone l'essere, di cui diventa semplicemente la negazione. Più interessante e problematico è concepire il nulla in maniera assoluta, come non essere niente : in tale concezione esso è indipendente dall'essere, e può anche servire a definirlo come `nonnulla'.
Il problema del non-essere assoluto fu introdotto in occidente nel secolo vi a.C. da Parmenide, che ne affermò l'impossibilità in base alla seguente dimostrazione: per definizione, il non-essere deve non essere niente; se però esistesse, esso sarebbe appunto il non-essere; ma niente può allo stesso tempo non essere ed essere. Questa dimostrazione è più sottile di quanto appaia a prima vista, ed è una prima versione dei paradossi che dovevano turbare i sonni dei logici per millenni. In particolare, in essa sono espliciti per la prima volta due aspetti fondamentali della logica classica: il principio di non contraddizione (``non si può negare ed affermare allo stesso tempo uno stesso predicato di uno stesso soggetto''), e l'equilibrismo semantico di confondere l'affermazione di una negazione (``essere il non-essere'') con la negazione di una affermazione (``non essere l'essere''). L'unica critica, benchè non da poco, che si possa oggi fare a Parmenide è di aver confuso la sintassi con la metafisica, e di non aver capito ciò che aveva dimostrato: non la contradditorietà del non-essere come entità, ma l'inconsistenza dell'esistenza come predicato.3
Non bisogna comunque essere troppo severi con Parmenide, benchè la sua incomprensione ontologica del non-essere abbia avuto il bel risultato di impedire per due millenni lo sviluppo di una concezione occidentale dello zero in matematica. Probabilmente la sua riflessione non era infatti altro che un tentativo di penetrare l'essenza degli avvenimenti linguistici che stavano avvenendo proprio a quei tempi nella lingua greca: da un lato, la progressiva presa di coscienza dei vari significati del verbo essere (eimi), complicata dall'introduzione di un suo uso esplicito come copula, che era fino ad allora sottointesa; dall'altro lato, la progressiva confluenza di due tipi diversi di negazioni del verbo (il controaffermativo ou per i modi oggettivi, e il proibitivo mh per i modi soggettivi o potenziali) in uno solo.4
Se questa teoria è corretta, essa potrebbe spiegare la refrattarietà del problema del non-essere, e più in generale dei problemi metafisici, alle soluzioni filosofiche: tali problemi sarebbero semplicemente sintomi ed espressioni di difficoltà del linguaggio, e come tali le loro `soluzioni' non potrebbero ovviamente trovarsi al suo interno. Per dirla alla Duchamp, in metafisica non ci sarebbero dunque soluzioni perchè non ci sono problemi: o meglio, i problemi stanno altrove, e le peculiarità del linguaggio (prima fra tutte l'incompletezza) sono la soluzione. Il che permetterebbe di annettere ai discorsi sul nulla tutti i discorsi metafisici, compresi quelli sul nulla.
Ma a questa conclusione (temporanea come ogni altra in filosofia) si è arrivati soltanto recentemente. Prima di allora, e nonostante la buona volontà di Parmenide, il non-essere non finì affatto nel cestino dei rifiuti della storia filosofica. In particolare, già nel secolo v a.C. il sofista Gorgia proponeva, nell'opera Sul non essere , un nichilismo radicale a tutti i livelli (realtà, conoscenza e linguaggio): ``niente è; se anche fosse, sarebbe incomprensibile; e se anche fosse comprensibile, sarebbe indicibile''.
Gli atteggiamenti dominanti nel pensiero occidentale nei confronti del non-essere furono invece codificati nel secolo iv a.C. da Platone e Aristotele, che coniugarono il rifiuto ontologico del non-essere con una sua accettazione epistemologica. In particolare, nel Sofista Platone ne introdusse una versione relativa (non-essere qualcosa) in contrapposizione alla versione assoluta (non-essere niente), e la pose a fondamento della negazione . E nella Metafisica Aristotele estese l'isomorfismo semantico tra essere e verità, già stabilito da Parmenide, anche a non-essere e falsità : ``è falso dire che l'essere non è, o che il non-essere è; è vero dire che l'essere è, e che il non-essere non è'' (G, 7, 1011b).
Dio nulla
La completa alterità del non-essere rispetto all'essere portarono sia Plotino (Enneadi , iii, 6, 7) che Agostino ( Confessioni , xii, 6, 2) ad identificarlo con la materia : questa si può infatti considerare come ciò che rimane degli esseri quando si faccia astrazione da tutte le loro determinazioni.
In maniera ancora più radicale, il non-essere come assoluta negazione dell'essere, e dunque qualcosa di completamente altro dall'universo, porta naturalmente alla sua identificazione con la divinità , e al perseguimento dell'unione con essa mediante l'autoannientamento mistico da un lato, e la distruzione del mondo propria di una tradizione che va dai Veda shivaitici all'Apocalisse cristiana dall'altro.
Una classica formulazione orientale dell'identificazione tra divinità e nulla è il taoismo, che definisce appunto il Tao in maniera puramente negativa. Ad esempio, secondo il Tao Tze Ching esso non è l'azione, l'impegno, la cultura, le parole, il sapere, lo studio, la ragione, il possesso, gli interessi, i desideri, l'affermazione, la stabilità, l'eccesso, la violenza, le armi, la guerra, la potenza, l'offensiva, l'alterigia, la durezza, la mascolinità, i viaggi, ... Ed è invece l'inazione, il vuoto, l'ignoranza, la negazione, il ritiro, la traquillità, la tolleranza, la semplicità, l'accettazione, il mutamento, l'umiltà, la discrezione, la passività, la calma, la pace, l'illuminazione, la debolezza, il basso, il molle, la diminuzione, la femminilità, la mansuetudine, la moderazione, la difensiva, ...
In occidente il nulla assurge a principio fondatore nel secolo iii d.C. con le Enneadi di Plotino, la cui filosofia si può facilmente condensare nell'equazione 0 = 1. Al Nulla egli arriva infatti attraverso astrazioni in due direzioni apparentemente divergenti, verso la forma pura da un lato e la materia indeterminata dall'altro, che spogliano l'essere di tutte le sue caratteristiche. Ma anche l'Uno che costituisce il principio di ogni cosa non può essere definito che negativamente, appunto come completamente altro rispetto all'essere. In tal modo Nulla e Uno risultano essere la coincidente essenza delle cose, ed in essi Plotino ritrova la libertà (come totale assenza di costrizioni), la bellezza (come assoluta perfezione), e la verità (come completa trascendenza).
A causa della sua doppia ascendenza, greca ed ebraica, la tradizione cristiana si trovò a soffrire di un atteggiamento ontologico schizofrenico verso il non-essere: da un lato essa lo rifiutava totalmente, sulla scia di Parmenide; dall'altro essa doveva accettarlo almeno parzialmente, come stato da cui il creatore era partito per la creazione dell'universo (i greci non avevano questo problema perchè il loro dio era un demiurgo, che plasmava ciò che già c'era, e non un creatore). La soluzione data al problema da Agostino fu salomonica: si poteva accettare il non-essere, ma solo come assenza di Dio, manifestata nel male , incarnata nel diavolo , e vissuta nel peccato (assegnando così un ruolo teologico alle categorie logiche del falso, del sofista e dell'errore).
Una posizione più possibilista fu esposta dall'umanista Carlo Bovillo (Charles de Bovelles) nel Libellus de nihilo , del 1509. Egli vide Dio e il nulla contrapposti come il necessario e l'impossibile, con la creazione situata a metà tra questi due poli, nella dimensione del possibile. Se prima della creazione Dio è solo e l'universo non è ancora altro che nulla, dopo la creazione Dio non è più solo e l'universo ha occupato una parte del nulla. E qui arriva l'imperituro colpo di genio: se la creazione occupasse tutto il nulla non rimarrebbe più nessuno spazio per Dio, e dunque il nulla è l'assicurazione sulla vita di Dio stesso. O, in termini più logici: ``se il nulla è, tutte le cose sono; se tutte le cose sono, Dio è; dunque se il nulla è, Dio è'' (ossia: se l'impossibile è, a maggior ragione il possibile è; se il possibile è, a maggiore ragione il necessario è; dunque se l'impossibile è allora il necessario è).
Ma ancora più radicale era già stato, nel secolo xiii, il mistico domenicano Maestro Eckhart: egli sosteneva che Dio è tutto, e dunque fuori di Dio non c'è che il nulla (Niht ûzer gote enist ); ma anche che Dio, in quanto contrario delle cose che sono, è esso stesso nulla di nulla (Er ist nihtes niht ). Le due dichiarazioni conciliano paradossalmente un radicale nichilismo e un globale panteismo: tutto è niente, ma niente è Dio, dunque tutto è Dio. Esse propongono anche una teologia negativa, secondo cui ogni essere è negazione dei rimanenti, e Dio è negazione di ciascun essere e dunque doppia negazione, cioè pura affermazione.
Nel secolo xv la teologia negativa approdò addirittura in Vaticano, quando il cardinale vicario Nicola Cusano (Nikolaus Krebs) arrivò a sostenere, ne La dotta ignoranza , che parlare di Dio in modo positivo lo riduce ad una creatura, e se ne può parlare soltanto in modo negativo. Il suo pensiero teologico attraversò tre momenti di successiva radicalizzazione: in una prima fase egli ritenne che, parlando di Dio, le negazioni sono più veritiere delle affermazioni (Dio è quindi infinito, cioè non -finito, immortale, immateriale, e così via); in una seconda fase Cusano indentificò Dio con la coincidenza degli opposti (allo stesso tempo Dio è e non è, è finito e infinito, e così via); in una terza fase Cusano unì i due approcci precedenti, e identificò Dio con la coincidenza di opposti negativi (Dio quindi nè è nè non è, non è nè finito nè infinito, e così via).
La teologia nichilista era comunque un pericoloso giocare col fuoco (sia del rogo che dell'inferno), e l'atteggiamento tollerante della chiesa nei confronti di Cusano fu puramente parentetico. Prima di lui Maestro Eckhart era finito sotto processo per eresia, aveva dovuto ritrattare le sue dottrine, ed era stato condannato ufficialmente dal papa (morendo nel frattempo, prima della fine del processo). Dopo Cusano, le velleità negative della teologia annegarono nel bagno di sangue dell'Inquisizione: esemplare in questo senso fu il caso del quietismo di Miguel de Molinos, che predicava l'autoannichilazione e l'unione col nulla, oltre a cose più piacevoli quali l'accettazione delle tentazioni sessuali e dell'opera del demonio, con la scusa che bisogna abbandonarsi totalmente alla volontà di dio (a suo onore, così egli fece coerentemente anche quando fu processato, non difendendosi e accettando tutte le accuse).
Nel secolo xx la concezione negativa della divinità ha preso le vuote forme della teologia della morte di Dio di Hamilton, Altizer e van Buren, che offre variazioni sul tema di Nietzsche: ``Dio è morto'' (a sua volta variazione sul tema di Plutarco: ``il grande Pan è morto''). Essa è stata intesa in vari modi, accomunati soltanto da una negazione dell'idea tradizionale di Dio: egli è oggi oscurato, o silente, o assente, o partito, o da qualche parte ma non nel mondo, o mai esistito; oppure è sintatticamente inesprimibile, o semanticamente vuoto e senza senso, o dialetticamente scomparso nella sintesi (incarnazione) di tesi (divinità) e antitesi (umanità). Il risultato di queste premesse è l'ossimoro della `teologia ateista': si deve vedere l'essenza dell'incarnazione nel passaggio dal divino all'umano; o, in assenza del Padre, ci si deve accontentare del Figlio (o, ancora meglio, di quella versione appropriatamente indebolita dell'onnipote nte che è il Nipote); o si deve ammettere che Dio non è ancora arrivato, ma continuare a sperare che arrivi, religiosamente ``aspettando God(ot)''; o si può essere credenti soltanto non credendo, o religiosi soltanto essendo secolari, o sacri soltanto essendo profani; ...
L'espressione più pregnante della morte di Dio è però forse non negli equilibrismi squilibrati di certi teologi, ma nella perifrasi letteraria del Padre Nostro di Ernest Hemingway in ``Un posto pulito, illuminato bene'' (dai Quarantanove racconti :
Nulla nostro, che sei nel nulla, sia santificato il tuo nulla, venga il tuo nulla, sia fatto il tuo nulla, dovunque nel nulla. Dacci oggi il nostro nulla quotidiano, e rimetti a noi i nostri nulla, come noi li rimettiamo agli altri nulla. E non ci indurre in tentazione, ma liberaci dal nulla. Amen.
O, analogamente, nel Salmo di Paul Celan:
Nessuno ci forma di nuovo
traendoci fuori da terra e fango,
nessuno parla alla nostra polvere.
Nessuno.
Tu sia lodato, Nessuno.
Per amor tuo fioriamo.
Al tuo cospetto.
Un nulla
eravamo, siamo, resteremo
fiorendo:
rosa del nulla
e di nessuno.
Divenire o non divenire?
Parmenide conciliava l'impossibilità del non-essere con quella del divenire: questo infatti richiederebbe un passaggio dal non-essere all'essere, ma ``dal nulla non si crea nulla'' (ex nihilo nihil fit ). Poichè il non-essere è necessario per il divenire, qualunque filosofia che accetti questo deve dunque fare i conti con quello.
Il primo dei moderni a farlo fu Georg Friedrich Hegel, nel 1812: nella Scienza della logica egli inaugurò un atteggiamento conciliatorio fra essere e nulla, accettandoli entrambi come necessarie premesse della contingenza, che altro non sarebbe che una loro partecipazione dialettica. In tale concezione l'essere e il nulla sono entrambi necessari per spiegare l'esistenza e la storia, che attivano un continuo passaggio dall'uno all'altro e viceversa.
La rivalutazione del nulla e la svalutazione dell'essere effettuati da Hegel erano ovviamente un rifiuto dell'eredità parmenidea, ma non il solo: Kant aveva mostrato che l'essere era in realtà inconoscibile, e l'idealismo aveva dedotto che allora era inutile postularlo. Su queste osservazioni si basò l'interpretazione che Friedrich Nietzsche diede nel 1888, nel Crepuscolo degli dei , della storia della filosofia occidentale come affermazione del nichilismo: il passaggio dal divenire all'essere aveva sì prodotto il peccato originale della sostituzione del mondo ideale della metafisica al mondo reale delle apparenze (``il mondo vero finì per diventare favola''), ma tutta la storia successiva si poteva leggere come un percorso di redenzione dall'essere, e di riaffermazione del non-essere. Quanto alla storia futura, essa avrebbe perfezionato varie forme di nichilismo: incompleto, in cui rimane ancora il bisogno di verità metafisiche (scientifica, morale, artistica); completo, dominato dallo struggimento del nulla; e classico, in cui un nuovo tipo di uomo (il superuomo, di cui Nietzsche si considerava il primo esempio) sarà in grado di accettare la completa mancanza di senso e il carattere caotico del mondo.
L'idea del nulla come fondamento dell'esistenza umana è stata ripresa nel 1929 da Martin Heidegger, in Che cos'è la metafisica? Non possiamo chiederci razionalmente che cosa sia il nulla, poichè questo presuppone che possa appunto essere qualcosa: i discorsi sul nulla non possono dunque far parte del linguaggio, della logica o della scienza, che sono tutte esclusivamente concentrate sull'essere. E neppure possiamo arrivare al nulla attraverso la totale negazione dell'essere, perchè questo presupporrebbe la possibilità di conoscere l'essere nella sua totalità, cosa certamente preclusa all'uomo. Ma è proprio questa impossibilità di percepire la totalità dell'essere, questa condanna all'incompletezza, che ci permette di arrivare alla intuizione del nulla, attraverso l'angoscia che essa genera. E questa angoscia esistenziale, oltre ad identificare negativamente nel nulla l'origine di tutto ciò che è oscuro e problematico nell'esistenza, ci rivela anche positivamente che l'esistenza è il nostro modo di stare al di fuori del nulla, ossia che il nulla definisce la possibilità della nostra identità.
Ne L'essere e il nulla , del 1943, Jean Paul Sartre riprende gli stessi temi, riferendoli però non più all'esistenza ma alla coscienza. Mentre l'essere è in sé , caratterizzato soltanto dall'essere ciò che è, la coscienza è per sé , cioè presente a se stessa: ma questa presenza richiede uno sdoppiamento in soggetto e oggetto, e dunque una separazione che può essere prodotta soltanto dal nulla. Ne derivano due conseguenze: anzitutto, poichè l'essere può esistere soltanto nella coscienza, il nulla è la condizione per la possibilità dell'essere, perchè lo è per la coscienza; inoltre, poichè la coscienza trova in sé la sua propria possibilità, l'essenza della condizione umana è fondata sul nulla (``l'uomo è l'essere per cui il nulla viene al mondo''). E questa essenza trova la sua realizzazione attraverso la libertà: essa è il mezzo attraverso cui l'uomo inventa continuamente la propria esistenza, proiettando se stesso dal nulla nel nulla, e mostrandosi dunque come ``una passione inutile''.
Se Nietzsche riteneva che il compimento del nichilismo richiedesse il pensiero dell'eterno ritorno, noi possiamo ritenere che il compimento di questa breve storia del nichilismo richieda la considerazione del pensiero di Emanuele Severino, testimonianza vivente dell'eterno ritorno: filosoficamente a Parmenide, e storicamente al Santo Uffizio (che egli sia stato messo all'indice e radiato dall'Università Cattolica, ma non arrostito, potrebbe però forse suggerire l'esistenza di un qualche divenire). In Essenza del nichilismo , del 1972, Severino sostiene che il pensiero occidentale è stato caratterizzato dall'accettazione non dell'essere (come comunemente si crede) ma del divenire temporale, e dunque del nulla da cui le cose vengono e a cui vanno. Il nulla e la mancanza dell'essere generano però rispettivamente angoscia e desiderio, che devono venir rimossi con la creazione di immutabili trascendenti: Dio, i valori e la volontà di conoscenza ( epistéme ). Ma queste soluzioni finiscono con l'essere ancora più soffocanti dei problemi che volevano risolvere, e sono allora rimpiazzate dalla scienza e dalla tecnica, che realizzano il divenire (fare e disfare le cose) senza appellarsi agli immutabili. Un'alternativa esiste, e consiste nell'accettare l'essere e l'eternità: il divenire si può allora interpretare come apparire e scomparire dell'eterno, invece che come passaggio dal nulla al nulla; e il tempo si può intendere come una soluzione escogitata da menti finite per approssimare l'eternità.5
3 Il vuoto della fisica
L'atomismo da un lato, e la quantizzazione dall'altro, sembrerebbero aver eliminato dall'arsenale della fisica atomica non solo lo zero, ma anche l'arbitrariamente piccolo. In realtà la presenza del nulla nella fisica moderna si è fatta addirittura più problematica e inquietante, ed esso è arrivato a svolgere un ruolo quasi altrettanto fondamentale, se non addirittura maggiore, della stessa realtà apparente.
Spazio e tempo
Il nulla fa la sua apparizione più scontata in fisica nello spazio vuoto , introdotto in oriente dal taoismo: nel Tao Tze Ching ( xi) si afferma che l'utilità delle cose, dai vasi alle abitazioni, sta non in esse ma nei vuoti che delimitano; e nel Chaung Tzu ( iii) si elogia il bravo macellaio che sa usare un coltello per decenni senza mai affilarlo, inserendolo fra gli interstizi vuoti ed evitando accuratamente la materia (carne ed ossa).
In occidente il vuoto fu considerato da Democrito lo scenario dell'azione degli atomi, ossia il contenitore della materia: questa concezione fu accettata da Epicuro, Lucrezio e gli stoici, ma rimase minoritaria fino alla sua ripresa da parte di Newton. La teoria prevalente nell'antichità e nel medio evo fu infatti quella di Platone e Aristotele, che definivano lo spazio come una qualità posizionale degli oggetti materiali, e la posizione di un corpo come il sistema delle sue relazioni con gli altri corpi: in tale concezione non ha senso parlare nè di spazio assoluto, nè tanto meno di spazio vuoto, ed il rifiuto di entrambi si tramandò da Aristotele fino ai razionalisti (Cartesio, Spinoza, Leibniz) e agli empiricisti (Locke, Berkeley, Hume), per continuare poi nell'idealismo (Hegel), nello spiritualismo (Bergson) e nell'esistenzialismo (Heidegger).
Nel 1687 Newton resuscitò il concetto di spazio assoluto come recipiente degli oggetti materiali, precisandone la struttura matematica di continuo tridimensionale, vuoto, statico ed euclideo. Esso divenne la concezione prevalente non solo nella fisica classica, ma anche nella filosofia moderna: mediando le posizioni razionalista di uno spazio puramente concettuale, ed empiricista di uno spazio puramente percettivo, Kant attribuì infatti allo spazio newtoniano la natura di intuizione a priori , ossia di paradigma della conoscenza umana del mondo esterno.
Con la relatività speciale di Einstein, nel 1905, si ritorna ad una concezione relazionale e operativa dello spazio, anche se da un punto di vista puramente matematico il distacco dallo spazio newtoniano non è troppo radicale: si ha ora un continuo quadridimensionale (per l'aggiunta del tempo), ancora vuoto, statico e piatto (senza curvatura), ma non più euclideo. Se si misura lo spazio in anni-luce, la formula per la distanza di un punto di coordinate (x,y,z,t) dall'origine è infatti
|
che ridiventa comunque euclidea se si suppone, come ha proposto Hawking sulla scia di Kant, che gli orologi misurino in realtà un tempo immaginario t = it¢, nel qual caso si ottiene
|
Un vero distacco dallo spazio newtoniano si ha invece nello spazio-tempo della relatività generale di Einstein, del 1915, che ha una struttura dinamica e una curvatura, dipendenti dalla materia che vi è in esso. L'assenza di materia, e dunque dello spazio-tempo vuoto , è possibile, ma la sua struttura non coincide necessariamente con quella statica e piatta dello spazio-tempo della relatività speciale: esistono infatti modelli cosmologici in cui la quantità di materia dell'universo è nulla, ma lo spazio-tempo è comunque dinamico e curvo. A prima vista questo può sembrare strano: è necessario raffigurarsi un cambiamento che avviene benchè non ci sia niente che può cambiare. Il dilemma si risolve assegnando allo spazio-tempo vuoto una tendenza alla dispersione di corpi che vengano introdotti in esso, e che abbiano massa troppo piccola per modificarne la struttura geometrica: questa tendenza si manifesta come una curvatura dello spazio-tempo vuoto, detta curvatura di Weyl (distinta dalla curvatura di Ricci prodotta dalla materia).
Energia
Una prima apparizione del nulla energetico si ha relativamente alla temperatura di un insieme di particelle, che è definita come la loro energia cinetica media: in particolare, lo zero assoluto è la temperatura alla quale l'energia cinetica media è nulla, ed il moto delle particelle è quindi mediamente `congelato' (misurato in gradi Celsius, lo zero assoluto ha il valore di -273°). La temperatura è ovviamente collegata allo stato della materia: più le particelle si muovono, meno stanno a posto, e più l'insieme va verso la volatilizzazione; viceversa, meno le particelle si muovono, più stanno a posto, e più l'insieme va verso la solidificazione. Poichè però la temperatura misura appunto soltanto una media, anche allo zero assoluto le particelle non sono completamente ferme, e dunque lo stato non è necessariamente solido: ad esempio, anche allo zero assoluto l'elio non solidifica (a meno di non aumentarne enormemente la pressione).
Se lo zero assoluto è il nulla della temperatura, il nulla di un campo si chiama vuoto energetico , ed è definito come il suo stato di energia minima. La parola `vuoto' è giustificata dal fatto che, ad esempio, l'energia del campo gravitazionale è proporzionale alla massa, e dunque in questo caso il vuoto energetico corrisponde all'assenza di materia, ossia al vuoto materiale, immutabile e senza struttura. Ma non sempre la minima energia corrisponde all'assenza di materia: ad esempio, se si inserisce all'interno di un forte campo elettrico `vuoto' una coppia di piastre parallele di carica opposta (o una coppia elettrone-positrone), tanto vicine da annullare fra esse il campo stesso, si sottrae al campo l'energia che prima era presente in quella zona. In casi di questo genere il vuoto energetico non è materialmente vuoto, ed esso diventa simile ad un mezzo elastico in cui le particelle si muovono, o addirittura di cui le particelle costituiscono le vibrazioni.
Come allo zero assoluto le particelle sono ferme, ma soltanto mediamente, così nel vuoto quantistico materiale le particelle non esistono, ma soltanto mediamente: in esso si formano continuamente coppie di particelle e antiparticelle (o anche, in maniera quasi fantascientifica, di corpi e di `anticorpi'), benchè esse durino soltanto un tempo inversamente proporzionale alla loro massa. A permettere che dal nulla eterno si crei materia di durata infinitesima, senza che sia comunque violata la conservazione dell'energia, è il principio di indeterminazione di Heisenberg, secondo il quale il prodotto fra la differenza osservabile di energia e la durata misurabile di un evento deve essere maggiore di un numero h > 0, detto costante di Planck: qualunque quantità di energia si può dunque prendere a prestito per creare materia, purchè questo avvenga soltanto per un tempo tanto piccolo da mantenere il prodotto inferiore ad h, e dunque da rendere l'energia non misurabile (così come si può rubare del denaro senza violare la conservazione del capitale, purchè lo si faccia soltanto per un tempo inferiore a quello intercorrente fra due controlli). Questo meccanismo, che potrebbe essere all'origine della formazione delle forze indotte dai campi, non è comunque in grado di spiegare la creazione dal nulla di oggetti non effimeri, quali corpi macroscopici o l'universo stesso.
Una possibile spiegazione di come si possa passare dal vuoto materiale al non vuoto, ossia generare il nonnulla universale dal nulla, sempre senza violare la legge di conservazione dell'energia, è stata proposta nel 1973 da Edward Tyron: basta assegnare al campo gravitazionale un'energia negativa, pari a quella positiva posseduta dalla materia (secondo la legge E = mc2 ); questo significa interpretare l'apparizione della forza gravitazionale come il prezzo da pagare per creare materia pur mantenendo l'energia totale dell'universo nulla, come essa è in un universo vuoto che precede la creazione.
Gli sviluppi recenti della fisica hanno dunque reso completamente obsoleto il detto che la natura aborre il vuoto (horror vacui ): in realtà, a livello sia microscopico che macroscopico il vuoto può essere considerato come la naturale culla dell'esistenza, il punto di partenza da cui nascono le forme sia istantanee che temporali della materia, a cui ora rivolgiamo l'attenzione.
Materia
A prima vista una quantità come la massa di una particella non può essere nulla, altrimenti la particella non potrebbe esistere come materia: e così è infatti nella fisica classica, dove la massa di un corpo è una sua costante. Ma nella relatività la massa apparente di una particella è determinata da due fattori: una massa costante detta `a riposo', e la velocità che ne provoca una dilatazione. Poichè una massa a riposo non nulla diventa infinita alla velocità della luce, solo particelle con massa a riposo nulla possono raggiungere tale velocità: i quanti di luce, o fotoni, sono dunque particelle con massa a riposo nulla, condannati al moto perpetuo a velocità della luce.
Il passo successivo oltre una massa nulla è la pura e semplice mancanza di materia, che si manifesta concretamente nei buchi . Ad esempio, come le correnti elettriche negative sono il risultato di elettroni liberi che si muovono in una certa direzione attraverso un conduttore, buchi di elettroni liberi che si muovono in direzione opposta creano correnti elettriche positive.
Questo fatto suggerisce la possibilità di una inversione dell'atomismo, sul tipo di quella tra figura e sfondo: invece di considerare la materia come costituita di qualcosa (particelle) che si muove nel vuoto, si può cioè pensare che essa sia costituita di niente che si muove nel pieno . Una prima formulazione di questa teoria, in cui il `pieno' era una forma di etere, fu proposta da Osborne Reynolds alla fine dell'800, in Un'inversione di idee come struttura dell'universo .
In una seconda formulazione, del 1929, il futuro premio Nobel per la fisica Paul Dirac propose di considerare la struttura dell'universo (ossia il vuoto quantistico) come costituita di un inosservabile mare di elettroni che realizzano tutti i possibili stati di energia negativa: se uno di essi lascia il suo posto a causa di un aumento di energia, si crea da un lato un elettrone libero con carica negativa ed energia positiva, e dall'altro un buco che viene percepito come un antielettrone, cioè un positrone con la stessa massa dell'elettrone ma con carica opposta, anch'esso con energia positiva; il ritorno di un elettrone libero in un buco viene allora percepito come la scomparsa di entrambi, cioè come l'annichilazione di una coppia particella-antiparticella; e l'antimateria viene interpretata come il buco lasciato dalla materia in temporanea e libera uscita dal pieno dell'energia negativa.
Anche nella relatività generale la materia è un buco in un pieno: più precisamente, una discontinuità del campo gravitazionale . Nei luoghi in cui si trova la materia il campo diventa infatti infinito, e cessa dunque di esistere: come a dire che l'esistenza fisica incomincia dove finisce quella matematica, e quella materiale dove cessa quella ideale; senza dimenticare però che solo l'esistenza matematica ed ideale (il campo) è misurabile, mentre quella fisica e materiale (la discontinuità) è invece una metamorfosi moderna dell'irraggiungibile noumeno kantiano.
Oltre alle discontinuità locali del campo gravitazionale, ne esistono di globali che sono note come buchi neri . Essi furono studiati per la prima volta nel 1783 da John Michell e nel 1799 da Pierre Simon de Laplace, e si basano su una osservazione molto semplice: una particella di massa m in moto circolare uniforme a velocità v su un'orbita di raggio r intorno ad un corpo di massa M è in equilibrio quando le forze centrifuga (dovuta alla velocità) e centripeta (dovuta all'attrazione gravitazionale) sono uguali, cioè
|
Per potersi distaccare dal corpo la particella deve avere una velocità superiore a quella di equilibrio: ma poichè la velocità massima consentita dalla relatività è quella della luce, cioè v = c, nessuna particella si potrà staccare dal corpo se
|
Se dunque tutta la massa M del corpo è concentrata in una sfera di raggio inferiore ad r, detto raggio di Schwarzschild, nessuna particella potrà sfuggire al corpo, e questo diventa appunto un buco nero. Il raggio di Schwarzschild è meno di 1 centimetro per la terra e circa 1,5 chilometri per il sole, quindi lontano dai valori attuali di migliaia di chilometri; il raggio delle stelle a neutroni, di circa 10 chilometri, è invece già dell'ordine di grandezza richiesta; ma è solo altamente probabile, e non assolutamente certo, che ci siano effettivamente dei buchi neri nell'universo, ad esempio nel centro dei quasar; nè è chiaro se il nostro universo sia esso stesso un buco nero, benchè il suo raggio sia della corretta grandezza richiesta dalla sua massa. Neanche che cosa succeda all'interno dei buchi neri è chiaro: Hawkins ritiene che essi convertano la loro massa in energia, e scompaiano gradualmente per evaporazione; Dyson che essi si comportino come universi indipendenti e separati dal nostro; altri ancora che essi diventino possibili canali di comunicazione con altri punti del nostro o di altri universi.
4 Lo zero della matematica
Il vuoto della fisica, come si è ormai capito, è molto lontano dall'idea pura che ne abbiamo intuitivamente, e per recuperare la quale ci volgiamo ora da ultimo alla matematica.
Numeri
La prima ovvia immagine del nulla in matematica è lo zero : tanto ovvia, che sorprende venire a sapere che esso è stato inventato due sole volte nella storia, dagli indiani e dai maya, e in entrambi i casi abbastanza recentemente.
La mancanza dello zero non si fece infatti sentire fino a quando si usarono sistemi additivi di rappresentazione numerica, come quelli egiziano, greco, romano o atzeco, che in origine avevano solo simboli per l'unità, le decine, le centinaia, ... (o, più in generale, in base b, per le potenze della base b0, b, b2, ...): ad esempio, per rappresentare il numero 2030 i romani scrivevano mmxxx, che registrava la presenza di due migliaia e tre decine, ma non l'assenza di centinaia e unità, ed era da interpretare come
|
Al vantaggio dei sistemi additivi, e cioè l'indipendenza dall'ordine degli addendi, si opponevano però sostanziali svantaggi: da un lato, la teorica necessità di infiniti simboli per le infinite potenze della base; e dall'altro, la (poco) pratica pesantezza della rappresentazione, che richiedeva troppe ripetizioni. Questa venne dapprima ovviata con l'introduzione di simboli per altri numeri, come i v e l romani, e poi dall'eliminazione delle ripetizioni di unità, decine, centinaia, ... mediante l'introduzione di simboli per i numeri fra 1 e 9 (o, più in generale, delle potenze della base b mediante simboli per i numeri fra 1 e b-1): si passò così ad un sistema additivo-moltiplicativo , che permetteva ad esempio di scrivere 2030 più semplicemente come
|
Il passo finale fu l'introduzione, da parte dei babilonesi nel 2500 a.C., di un sistema posizionale (in base 60), che eliminava ogni menzione delle potenze della base mediante la convenzione di rappresentarle in un ordine fisso. In questo sistema sorge la necessità di indicare la mancanza di una potenza della base, e dunque di aggiungere ai simboli per i numeri fra 1 e b-1 anche un simbolo per lo zero, pena la confusione tra numeri quali 2300, 2030, 2003, 230, 203, 23, ... Ma i babilonesi si adattarono a convivere con la confusione: solo nel secolo iv a.C. i loro eredi seleucidi introdussero un simbolo per lo zero, e anche allora unicamente fra cifre, e non alla fine del numero; e solo nel secolo ii d.C. Tolomeo incominciò ad un usare un simbolo per lo zero (l'omicron o, iniziale di ouden, `vuoto') anche in posizione terminale (come pura notazione di assenza), benchè mai da solo (come presenza di un numero indipendente).
Anche i cinesi arrivarono ad un sistema posizionale (in base 10), menzionato a partire dal secolo iii a.C. Nel loro caso la confusione fu in parte evitata dal trucco di usare alternativamente due sistemi di numerali paralleli, che indicavano i numeri con sbarre rispettivamente verticali e orizzontali. Ad esempio, essi scrivevano 23 e 32 come = ||| e º ||, e dunque potevano distinguere 23 da 203, 230 e 2030, perchè questi ultimi venivano scritti come || ||| (pericolosamente simile a |||||), || º e = º , anche se rimaneva ancora un'ambiguità fra 23, 2003 e 2300. La prima menzione di un simbolo per lo zero in Cina è del 1247, anche se l'abaco condusse naturalmente ad un uso implicito dello zero nei calcoli.
Il primo sistema posizionale (in base 10) completo dello zero fu introdotto dagli indiani verso il 500 d.C. Nel manoscritto Bakhshali lo zero è indicato con · ed è chiamato sunya , che significa `vuoto': dalla sua traduzione araba sifr deriva la parola `cifra'; dalla successiva traduzione latina cephirum deriva l'italiano zevero , che poi divenne zero . Oltre che come zero esso funzionava anche da variabile, il che ha una certa logica: l'attuale mancanza di qualcosa si può infatti intendere come la possibile presenza di qualunque cosa!
Ad un sistema analogo a quello indiano (ma in base 20) arrivarono anche i maya, nella seconda metà del primo millennio. Essi avevano due tipi di rappresentazione: il primo usava tre soli simboli, e cioè una conchiglia vuota (chiamata xok , `vuoto') per lo zero, un punto · per l'uno, e una linea - per il cinque; il secondo, in accordo con la base del sistema, usava invece venti facce di divinità.
La forma attuale dello 0 ci arriva dagli arabi: essa è sia una stilizzazione del · indiano, che una deformazione del \bigcirc indicante un buco, che (forse) una rappresentazione dell'uovo generatore (una immagine appropriatamente adeguata agli sviluppi insiemistici, in cui l'analogo dello zero è effettivamente l'unico costituente di tutti gli oggetti). Come le altre cifre decimali, lo zero venne introdotto in Europa dapprima da papa Silvestro ii, che ne era venuto a conoscenza in un suo viaggio in Spagna nel 967, e poi nel 1202 da Fibonacci nel suo Liber abaci , non senza resistenze e scontri fra abacisti e algoristi, rispettivamente favorevoli al vecchio abaco e alla nuova notazione algebrica: nel 1299 la città di Firenze passò un'ordinanza che proibiva l'uso dei nuovi numerali perchè essi erano più facilmente falsificabili di quelli romani (ad esempio, cambiando 0 in 6 o 9), e un editto analogo fu ancora promulgato nel secolo xv a Francoforte.
Naturalmente, una volta introdotto lo zero diventa l'elemento neutro della somma, e permette l'annichilazione dei numeri e dei loro inversi come se fossero particelle e antiparticelle, secondo la legge
|
Esso può anche diventare oggetto di adorazione da parte di sette, come nel romanzo Archeologia dello zero di Alain Nadaud, o titolo e soggetto di una poesia, come nella seguente trasposizione antonimica de L'infinito leopardiano, di Domenico Garelli:
Mai odioso sarà quell'imo
piano,
e quell'erbetta, che a sì picciol tutto
dello zenit primier l'udito ammette.
Là vagando e ascoltando, limitati
tempi al di qua da questo, e animaleschi
rumori, e superficialissimo fracasso
colpiscono i miei sensi; onde di molto
la mente s'incoraggia. E se la pioggia
vedo spruzzar quegli animali, io questo
limitato rumor da quel tacere
vengo distingüendo: e oblio l'istante,
le vive annate, le passate e morte
ed i loro silenzi. E fuor di quella
piccolezza galleggia il morir mio:
e navigar m'è amaro in questo stagno.
Punti
L'analogo geometrico dello zero è ovviamente il punto , che Euclide definiva ap-punto come ``ciò che non ha parti'': che poi anche due punti, ovviamente ancora senza parti, dovessero allora essere secondo la sua definizione un solo punto, non sembrava preoccuparlo. In ogni caso, l'intera geometria è costruita a partire dagli evanescenti punti: forse nichilisticamente, ma certo non inconsistentemente, visto che enti che non hanno parti possono benissimo essere le parti di altri enti (spazi e figure, unidimensionali o pluridimensionali), che hanno dunque parti.
Se il punto è il nulla geometrico, un punto mancante è un buco a zero dimensioni : una doppia immagine del nulla. E se l'infinito è il contrario aritmetico dello zero, la continuità è il contrario geometrico del buco a zero dimensioni. La continuità della retta (che non è altro che una curva di curvatura nulla) è stata una delle ossessioni dei matematici dai tempi dei pitagorici, e una buona parte dello sviluppo dei sistemi numerici si può vedere come il tentativo di colmare sempre più buchi di quel vero e proprio colabrodo che è risultata essere la retta razionale.
A prima vista sembra infatti che non si possa inserire niente fra i razionali, perchè essi sono già ben densi: fra due qualunque di essi ne esistono sempre altri (ad esempio, fra a e b ci sta almeno [(a+b)/ 2]). Ma la prima impressione, come spesso succede, è sbagliata: se ad esempio si dividono i razionali in due classi disgiunte e non vuote A e B, ponendo a sinistra tutti quelli il cui quadrato è minore di 2, e a destra quelli il cui quadrato è maggiore di 2, non c'è nessun razionale maggiore di tutti gli elementi di A e minore di tutti gli elementi di B; in altre parole, c'è un buco sulla retta razionale, il che è un altro modo di dire che non esiste un razionale il cui quadrato sia 2. Anzi, si scopre poi che se si dividono i razionali in due classi disgiunte e non vuote A e B, tali che ogni elemento della prima è minore di ogni elemento della seconda, allora quasi sempre esse definiscono un buco, nel senso che quasi mai A ha un massimo, o B ha un minimo.
Per rimediare alla situazione, ovvero per completare la retta razionale, si sono introdotti i numeri reali , i quali sono stati definiti da Richard Dedekind nel 1872 proprio come coppie (A,B) del tipo appena descritto: in particolare, la coppia formata dai razionali i cui quadrati sono rispettivamente minori o maggiori di 2 definisce un numero che si indica con Ö2. Il mondo reale è certo più completo di quello razionale (con buona pace di Hegel, per il quale razionale e reale coincidevano), nel senso preciso che se si ripete il procedimento di dividere i reali in due classi disgiunte e non vuote A e B, tali che ogni elemento della prima è minore di ogni elemento della seconda, allora esse non definiscono mai un buco: o A ha un massimo, o B ha un minimo.
Neppure il mondo reale è però completo in un senso più forte: esistono cioè A e B del tipo precedente che non ammettono un numero reale maggiore di ogni elemento della prima, e minore di ogni elemento della seconda. Un tipico esempio si ottiene ponendo in A i reali minori o uguali di 0, e in B quelli maggiori di esso: un numero come quello richiesto sarebbe un esempio di ciò che Leibniz chiamava infinitesimo , cioè una quantità positiva arbitrariamente piccola ma non nulla. La vita degli infinitesimi è stata movimentata: essi furono usati intuitivamente per la prima volta da Fermat nel 1629; ritenuti ``una trave nell'occhio del matematico infedele'' dal vescovo Berkeley nel 1734; eliminati a partire dal 1841 da Weierstrass, mediante la riformulazione dell'analisi in termini di e e d; dichiarati ``un virus colerico che infetterebbe la matematica'', e dimostrati impossibili, da Cantor nel 1887; e confermati tali da Russell nel 1903. Ma nel 1965 Abraham Robinson notò che era invece possibile definire consistentemente gli infinitesimi, e con essi i numeri iperreali : come intorno ad ogni razionale sta una nuvola di irrazionali, così intorno ad ogni reale si crea una nuvola di iperreali non reali, che distano da esso per un infinitesimo; e come i reali coprono i buchi della retta razionale, così gli iperreali coprono quelli della retta reale.
Ma anche la retta iperreale ha i suoi buchi: ad esempio, come non c'erano reali maggiori di 0 e minori di ogni reale positivo, così non ci sono iperreali maggiori di 0 e minori di ogni infinitesimo positivo. John Conway ha dunque proposto nel 1976 di continuare il processo all'infinito e oltre, senza sosta, in modo da eliminare via via buchi sempre più evanescenti, per arrivare infine (cioè mai) ad una retta di numeri surreali assolutamente completa.6 La cosa interessante è poi che è possibile definire sui numeri surreali operazioni di somma e prodotto, in modo tale che esse estendano le analoghe operazioni sui numeri razionali o reali, e ne conservino le proprietà solite (di campo ordinato).
Dopo aver inseguito e raggiunto il miraggio di una retta completamente senza buchi, possiamo ora correre dietro al miraggio inverso, un insieme unidimensionale di punti che sia cioè completamente bucato. Una possibile soluzione sta nel richiedere che fra due punti qualunque ci sia non solo un buco a zero dimensioni (un punto), ma uno ad una dimensione (un segmento); e, per evitare soluzioni ovvie quali l'insieme degli interi, richiediamo inoltre che l'insieme abbia anche molti punti, ad esempio tanti quanti i numeri reali stessi. Una bella soluzione al problema è la cosiddetta polvere di Cantor , che si ottiene nel modo seguente: si prende un segmento, lo si divide in tre parti uguali, e si cancella quella centrale; si divide poi ciascuno dei segmenti rimanenti in tre parti, e si cancellano quelle centrali; e così via. In tal modo si polverizza il segmento iniziale, ma rimane comunque una quantità di punti pari a quella dei numeri reali stessi, perchè ogni punto rimasto è univocamente determinato da, e determina, il numero reale fra 0 ed 1 il cui sviluppo binario ha: come prima cifra, 0 se il punto sta nel terzo di sinistra del primo segmento, e 1 se sta in quello di destra; come seconda cifra, 0 se il punto sta nel terzo di sinistra del precedente segmento, e 1 se sta in quello di destra; e così via.
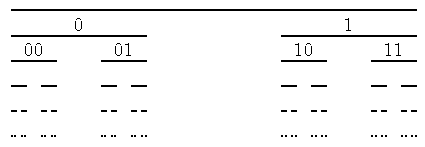
Un procedimento simile si può fare ad esempio con triangoli e cubi al posto di segmenti, e si ottengono rispettivamente oggetti completamente bucati a due o tre dimensioni, definiti in maniera analoga a quelli unidimensionali, e chiamati rispettivamente gaschetta di Sierpinski 7 e spugna di Menger . Questi oggetti non sono soltanto pure curiosità: essi sono anzi esempi di figure geometriche piuttosto in voga dette frattali , la cui proprietà caratteristica è di essere autosimili (tali cioè che ogni loro parte ha la stessa struttura del tutto), e che hanno trovato applicazioni nella descrizione di fenomeni naturali finora refrattari alla trattazione matematica, dalle nuvole alle coste.
In matematica i buchi nelle superfici chiuse a due dimensioni, lungi dall'essere inutili divertimenti, si sono poi rivelati essenziali per il famoso teorema di classificazione di Möbius del 1861, che nel più puro spirito taoista riduce l'essenza topologica di tali superfici alla struttura del vuoto in esse presente. Più precisamente: ogni superficie chiusa, pensata come se fosse di gomma, si può deformare tirandola o gonfiandola senza romperla in modo da farla diventare o una sfera (senza buchi), o una sfera con un numero finito di manici (ciascuno dei quali contribuisce un buco), o una sfera con un numero finito di buchi circolari rimossi e sostituiti con una striscia di Möbius;8 e questi tipi di superfici sono fra loro irriducibili, nel senso che nessuna di esse può diventare una delle altre mediante trasformazioni del tipo descritto. Per fare qualche esempio da manuale (di cucina): un bicchiere ed una pagnotta sono topologicamente delle sfere senza buchi, una tazza e una ciambella (ovviamente, col buco) sono sfere con un manico, e una bottiglia di Klein (una suppellettile peraltro poco presente nelle cucine non surrealiste, essendo costituita da una bottiglia il cui collo rientra all'interno e si congiunge al fondo) è una sfera con un buco circolare sostituito da una striscia di Klein.
Insiemi
L'analogo insiemistico del punto senza parti è l'insieme vuoto senza elementi, che si indica con Æ. Questa volta però i matematici moderni, più smaliziati di Euclide, hanno introdotto un assioma di estensionalità (una versione del principio degli indiscernibili di Leibniz), che identifica fra loro tutti gli insiemi con gli stessi elementi: diversamente dai punti, c'è dunque al più un insieme vuoto.
Che poi ce ne sia almeno uno, e dunque esattamente uno, si può dimostrare facilmente: basta dividere tutti gli insiemi in due classi N e V, ponendo nella prima quelli non vuoti, e nella seconda i rimanenti; se l'insieme vuoto esiste, non c'è niente da dimostrare; se invece l'insieme vuoto non esiste, allora V è l'insieme vuoto che cercavamo. Naturalmente, una tale dimostrazione è più umoristica che matematica: nella pratica l'esistenza dell'insieme vuoto viene assunta come primo assioma, per poter iniziare da qualcosa (il nulla!) la costruzione dell'intero edificio.
Poichè però questi discorsi rischiano di essere troppo astratti, prima di procedere oltre è bene mostrare una figura dell'insieme vuoto per illustrarne visivamente la struttura:
Figure 1: L'insieme vuoto.
Come la geometria è costruita a partire dai punti, anche la teoria degli insiemi (e dunque tutta la matematica moderna, che su di essa si basa) è costruita a partire dall'insieme vuoto, e si riduce letteralmente ad un edificio di pure forme che si dissolve in ultima analisi nel nulla: allo stesso modo, si rimane con niente in mano se si cerca l'essenza della cipolla pelandola (Ibsen, Peer Gynt ; Pirandello, Vestire gli ignudi ), o del carciofo sfogliandolo (Wittgenstein, Ricerche filosofiche ).
La riduzione dell'aritmetica alla teoria degli insiemi, e dunque dei numeri al nulla, è stata compiuta da Gottlob Frege nel 1884, e semplificata da John von Neumann nel 1923. L'idea ovvia è di identificare lo zero con l'insieme vuoto; meno ovvio è definire l'uno come un insieme privilegiato con un solo elemento, cioè lo 0, e più in generale un numero con l'insieme dei suoi predecessori. Simbolicamente, il processo è generato dalle due regole
|
da cui si ricavano le seguenti forme esplicite per i primi numeri:
|
Non c'è però nessun motivo per fermare la potenza generativa del nulla, che costruisce gratuitamente sostanza a partire dalla pura forma, e infatti Georg Cantor ha esteso nel 1883 l'aritmetica del finito in una aritmetica del transfinito, che comprende oltre ai numeri interi anche gli ordinali transfiniti , i cui primi esempi sono i seguenti:
|
Ovviamente, una volta innescato, il processo esplode in un Big Bang numerico che prosegue senza sosta, generando via via infiniti sempre più complicati, benchè tutti riducibili in ultima analisi al nulla:
|
Ma, come dai numeri interi si passa successivamente ai numeri razionali, reali, iperreali e surreali, così si può pensare di fare per gli ordinali. E anche in questo caso ci si può porre il problema di eliminare successivamente tutti i buchi `esterni', benchè l'impresa appaia ora in qualche modo paradossale, a causa del fatto che i numeri stessi sono costituiti soltanto di buchi `interni': si tratta cioè di stipare il più possibile oggetti completamente bucati, in modo che non rimanga fra loro nessun buco. L'idea è comunque di ottenere un sistema che in qualche modo contenga tutti i numeri , e la soluzione trovata da Conway è stata di estendere appunto la costruzione dei numeri surreali. Anzi, questa volta si possono definire tutti i numeri in un colpo solo, mediante due semplici regole che portano all'estremo limite il metodo di Dedekind:
- se A e B sono insiemi di numeri tali che ogni elemento di A è minore di ogni elemento di B, allora (A,B) è un numero
- un numero (A,B) è minore o uguale di un numero (C,D) se ogni elemento di A è minore di (C,D), e ogni elemento di D è maggiore di (A,B).9
Le due regole permettono di generare tutti i numeri ordinali e surreali, e in particolare dunque gli interi, i razionali, i reali e gli iperreali, oltre ad una cornucopia di altri numeri mai visti prima. Ad esempio:
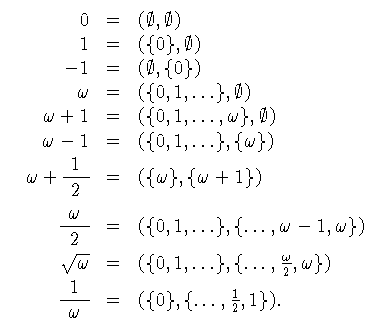
noltre, è possibile definire sui numeri, una volta per tutte, operazioni di somma e prodotto che estendono quelle sui numeri (sur)reali, e che hanno le proprietà solite (di campo ordinato). E in questo modo si arriva alla fine della storia, o almeno di questa: si dimostra infatti che ogni insieme che ammetta operazioni di somma e prodotto con le proprietà solite si può pensare immerso nella classe di tutti i numeri, in modo analogo a quello con cui i razionali sono immersi nei reali, i reali negli iperreali, e gli iperreali nei surreali.
Sembra dunque che, ottenuti tutti i numeri, non rimanga niente altro da aggiungere: il che però suona proprio come dire che rimane ancora del nulla da eliminare! Ma cercare di spingere oltre il processo che ci ha portati a tutti i numeri è pericoloso, perchè richiederebbe la considerazione in (A,B) di classi arbitrarie A e B che non sono necessariamente insiemi: il che in genere è foriero di paradossi e inconsistenze. È allora solo come metafore che è possibile considerare due limiti estremi: da un lato W, l'infinito assoluto che sta oltre ogni numero; e dall'altro ¥, l' infinito potenziale che sta sopra ogni numero finito, ma sotto ogni numero infinito. Nè W nè ¥ sono numeri: se W lo fosse, allora dovrebbe essere W < W perchè W è maggiore di ogni numero; e se ¥ lo fosse, allora sarebbe o finito o infinito, e in entrambi i casi ¥ < ¥, nel primo perchè ¥ è maggiore di ogni numero finito, e nel secondo perchè è minore di ogni numero infinito. Metafore o no, si può comunque dimostrare formalmente l'equazione
![]()
n misterioso legame quasi esoterico fra i tipi di infinito che il vuoto ha generato, e dunque una suggestiva conclusione della nostra indagine del nulla.
Bibliografia
- Robert Martin Adams, Nil: episodes in the literary conquest of void during the nineteenth century , Oxford University Press, 1966.
- Donald Knuth, Surreal numbers , Addison Wesley, 1974.
- John Conway, On numbers and games , Academic Press, 1976.
- Benoît Mandelbrot, Gli oggetti frattali , Freeman, 1977 (Einaudi, 1987).
- Brian Rotman, Signifying nothing. The semiotics of zero , Stanford University Press, 1987.
- Simon Saunders e Harvey Brown, The philosophy of vacuum , Clarendon Press, 1991.
- Roberto Casati e Achille Varzi, Buchi e altre superficialità , M.I.T. Press, 1994 (Garzanti, 1996).
- Sergio Givone, Storia del nulla , Laterza, 1995.
- Franco Volpi, Il nichilismo , Laterza, 1996.
Footnotes:
1 Le due parole risultano quasi anagrammatiche, scartando la doppia s e identificando i quasi omofoni n e i: una soluzione più che accettabile ai tempi di Omero, quando la lingua greca non era ancora scritta.
2 In semiologia si distinguono, a partire da Peirce, tre tipi di rappresentazione del segno: l'indice punta al suo referente mediante un rapporto causale, quale l'orma ha con la persona che l'ha lasciata; l'icona mediante una similarità, quale la figura ha con l'oggetto raffigurato; il simbolo mediante una semplice convenzione, quale la parola ha con il suo significato.
3 Nella logica moderna, l'argomento di Parmenide si riformula definendo l'esistenza E come
|
ossia x esiste se ha qualche proprietà (una definizione del second'ordine). Se E fosse un predicato allora anche la sua negazione ØE lo sarebbe, e
|
contraddizione. L'argomento di Parmenide era semplicemente che se l'ipotesi ØE(x) è contradditoria come negazione di un'affermazione (``x non è l'essere''), lo è anche come affermazione di una negazione (``x è il non-essere''). Oggi diciamo invece che sia l'essere (E) che il non-essere (ØE) sono contradditori, se intesi come predicati (e infatti essi sono quantificatori: un'inversione che si manifesta graficamente nel passaggio da E a $).
4 Nella logica moderna vari usi del verbo essere, confusi nel linguaggio naturale, vengono diversificati mediante operatori distinti: veridico (x è vero: \models x), esistenziale (x esiste: $x), copulativo (x è P : P(x), dunque con la copula sottointesa, come nel greco antico), di identità (x è y : x = y), di appartenenza singolare (x è un y : x Î y) e plurale (gli x sono y : x Í y). Inoltre, si usano due negazioni, una linguistica (Ø) e una metalinguistica (non), il cui significato relativo è determinato dalla definizione di verità di Aristotele-Tarski: ``x è ØP''significa ``x non è P''.
5 Come Flatlandia narra convincentemente, un essere tridimensionale può percepire anche staticamente un oggetto spaziale tridimensionale, ma solo dinamicamente un oggetto spazio-temporale quadridimensionale.
6 Utilizzando la nozione di numero ordinale introdotta in seguito, si possono distinguere i vari numeri in base alla lunghezza dello sviluppo decimale dopo la virgola: gli interi hanno sviluppo nullo, i razionali finito (o periodico), i reali di lunghezza w, gli iperreali di lunghezza 2 ·w, e i surreali di lunghezza W, pari cioè a tutti gli ordinali.
7 Un oggetto simile alla gaschetta di Sierpinski si ottiene dal triangolo di Pascal quando si cancellino da esso tutti i suoi elementi pari.
8 Una striscia di Möbius si ottiene prendendo una striscia di carta rettangolare ed incollandone due lati opposti, dopo averle fatto fare mezzo giro: poichè la striscia così ottenuta ha un solo lato ed un solo bordo, essa può dunque essere sostituita ad un buco circolare.
9 Ovviamente, dire che x è maggiore (o uguale) di y significa dire che y è minore (o uguale) di x, e dire che x è minore di y significa dire che x è minore o uguale, ma non maggiore o uguale, di y.
Da: http://www.vialattea.net/odifreddi/nulla.htm

